2019牛客D
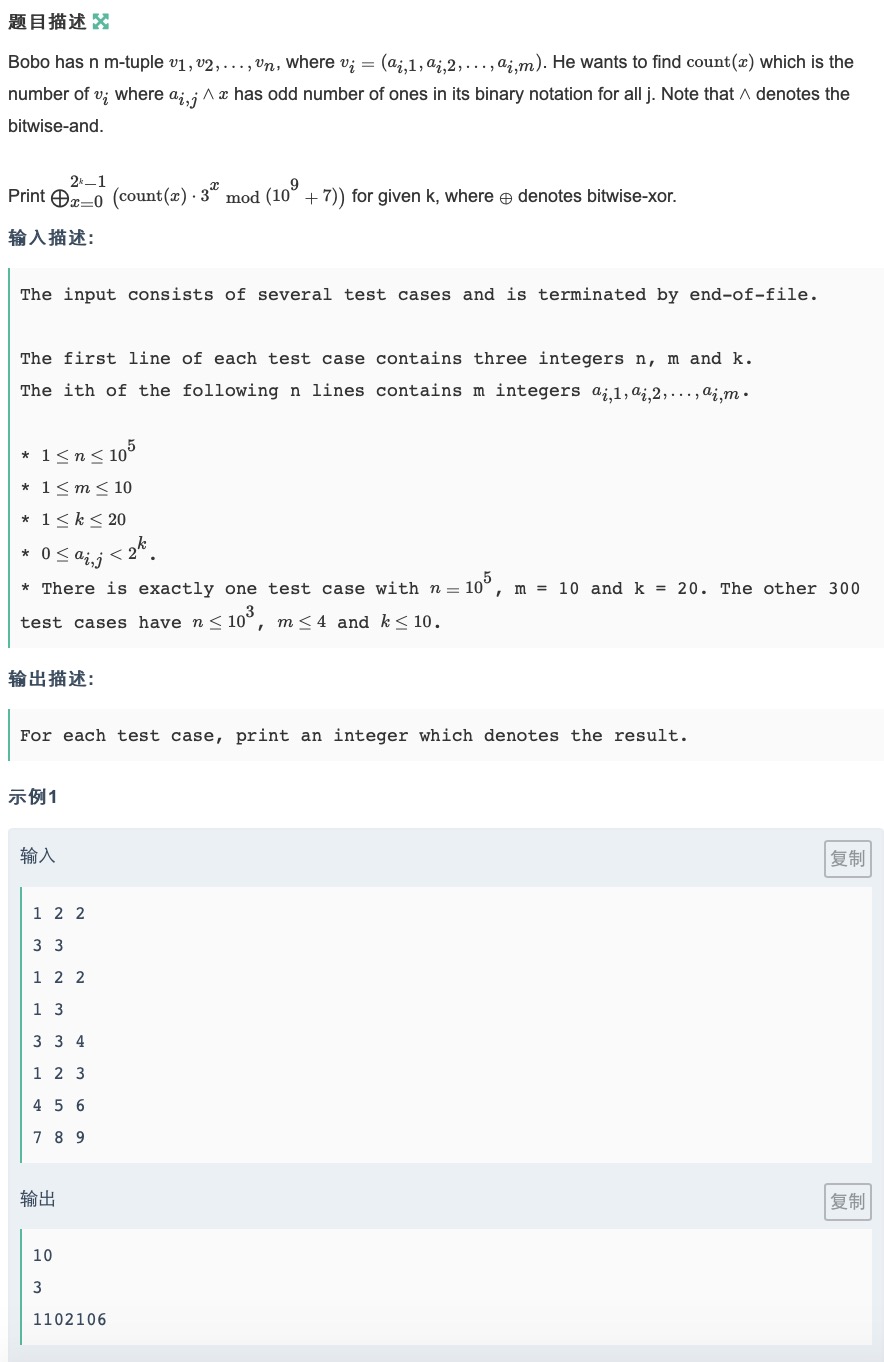
简单化简一下要我们求的东西
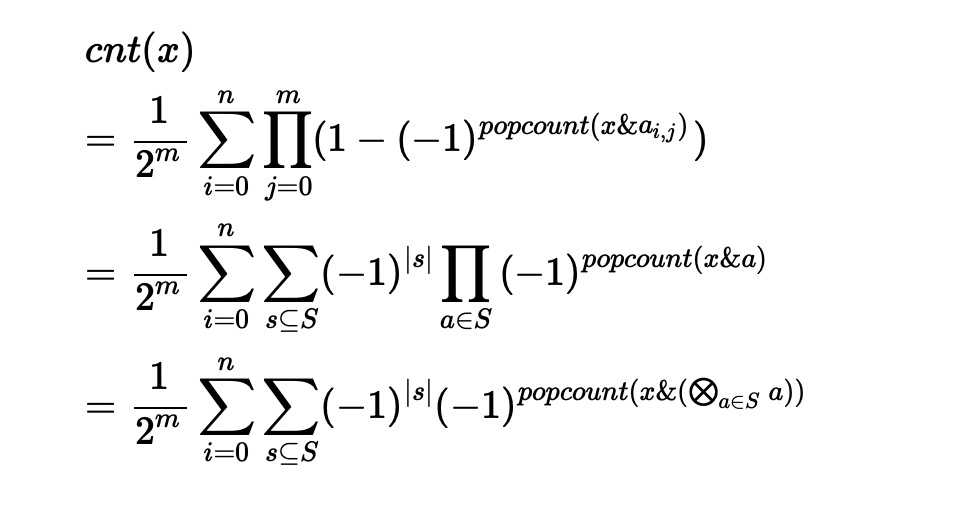
其实这个就是异或卷积fwt的定义,把前两个求和合成一个求和,用-1的|S|次方构造原数列,跑一次fwt就是答案
#include<bits/stdc++.h> using namespace std; int sum[1<<10],cnt[1<<20]; int mod=1e9+7; int qpow(int a,int b){ int ret=1; while(b){ if(b&1) ret=1ll*ret*a%mod; a=1ll*a*a%mod; b>>=1; } return ret; } //求卷积a[]=>fwt(n,0)=>fwt[]=>fwt(n,1)=>a[] //fwt(x$y)=fwt(x)*fwt(y);$代表|,&,^ void fwt(int *a, int n, int f) { for (int k = 1; k < n; k <<= 1) for (int i = 0; i < n; i += (k << 1)) for (int j = 0; j < k; j++) if (f == 1) { int x = a[i + j], y = a[i + j + k]; //&:a[i+j]+=a[i+j+k]; //|:a[i+j+k]+=a[i+j]; a[i + j] = x + y; a[i + j + k] = x - y; } else { int x = a[i + j], y = a[i + j + k]; //&:a[i+j]-=a[i+j+k]; //|:a[i+j+k]-=a[i+j]; a[i + j] = (x + y) / 2; a[i + j + k] = (x - y) / 2; } } int main(){ ios::sync_with_stdio(false); int n,m,k; while(cin>>n>>m>>k){ for(int i=0;i<1<<k;i++) cnt[i]=0; for(int i=0;i<n;i++){ int a[10]; for(int j=0;j<m;j++) cin>>a[j]; for(int s=0;s<1<<m;s++){ if(s!=0) sum[s]=sum[s&(s-1)]^a[__builtin_ffs(s)-1]; if(__builtin_parity(s)) cnt[sum[s]]--; else cnt[sum[s]]++; } } fwt(cnt,1<<k,1); int ans=0, rev=qpow(1<<m,mod-2),mul=1; for(int i=0;i<1<<k;i++){ ans^=1ll*mul*cnt[i]%mod*rev%mod; mul=3ll*mul%mod; } cout<<ans<<endl; } }