美团笔试

2020-04-16

字数统计: 1.4k字 | 阅读时长≈ 6分

next hexonext butterfly volantis yearn yilia shoka indigo apollo landscape cactus matery icarus fluid material

2020/4/16美团笔试不多说，美团的题真的出的好，尽管我没有做完，但是体验挺好的。 # 第一题 n个人，每个人m个科目，只要一个人某科是最高分或者最高分之一，我们就要为他颁奖，每个人最多颁奖一次，问最需要多少次颁奖统计最值就ok了 # 第二题输入a,b,x,m, 你讲进行不断的迭代x = (a*x+b)%m, 问x的循环节是多少， m<1e5 暴力枚举2*m轮，枚举的时候

for(int i=0;i<2*m;i++){
  x = (a*x+b)%m;
  pre[x]=i;
}
cout<<2*m-pre[(a*x+b)%m]<<endl;

# 第三题有一个长度为n的数组，将他们两两组合为数对，会得到$n^2$个数对，数对比大小的时候先比较第一个值，如果第一个值相同，则按照第二个值排序，问排名第k的数对是哪一个

我二分答案的，先二分第一个值，然后二分第二个值,千万注意存在数值相同的情况, 我们考虑数对(x,y)的最大排名，显然我们用upper_bound找到x和y的位置，然后lower_boundx的位置，然后就能根据这三个值算出(x,y)的排名了

第四题

伪中位数，我们定义排名为$\lfloor\frac{n+1}{2}\rfloor$的数为伪中位数，给你一个数组a[]和一个数k,问你至少在a中添加多少个数一个k成了a[]的伪中位数，我们统计小于k的数x个，大于k的数y个，然后执行下面的程序，去模拟这个过程，不知道为啥，我这题没有通过，卡在了56%的位置,挺遗憾的,就差一点点就AK了

x // 小于k的数的个数
y // 大于k的数的个数
n // 数组长度
int f(int x,int y,int n){
  while(x+y<n-1){
    if(x<y) x++;
    else y++;
  }
  int ans = 0;
  while(true){
    if(x==y)break;
    if(x==y-1)break;
    if(x<y) x++;
    else y++;
    ans++;
  }
  cout<<ans<<endl;
}

第五题

输入串S和T，在S中选一个子序列s，在T中选一个子串t，问有多少个选法，使得s=t，答案对1e9+7取模
设dp[i][j]为S[0:i], T[0:j] 且必须选T的结尾的字符的情况下的方案数量，那么

1 2	dp[i][j] = S[0:i] 中S[?]==T[j]的个数再加上下面的 dp[i][j] += dp[k-1][j-1] 当且仅当k<=i且S[k]==T[j]

现在我们就可以写出一个$n^3$复杂度的算法了

考虑优化它，设Sum[i][j] 为 dp[k-1][j-1] 在k<=i且S[k]==T[j]的和，然后推导

1 2	Sum[i][j] = Sum[i-1][j] 当S[i]==R[j]的时候 Sum[i][j] = Sun[i-1][j] + dp[i-1][j-1]

现在我们得到了双线dp，这两个dp互相向后推导，最终得出答案,复杂度$n^2$

2020/4/19更新

感谢指正，我想复杂了，我还是太菜了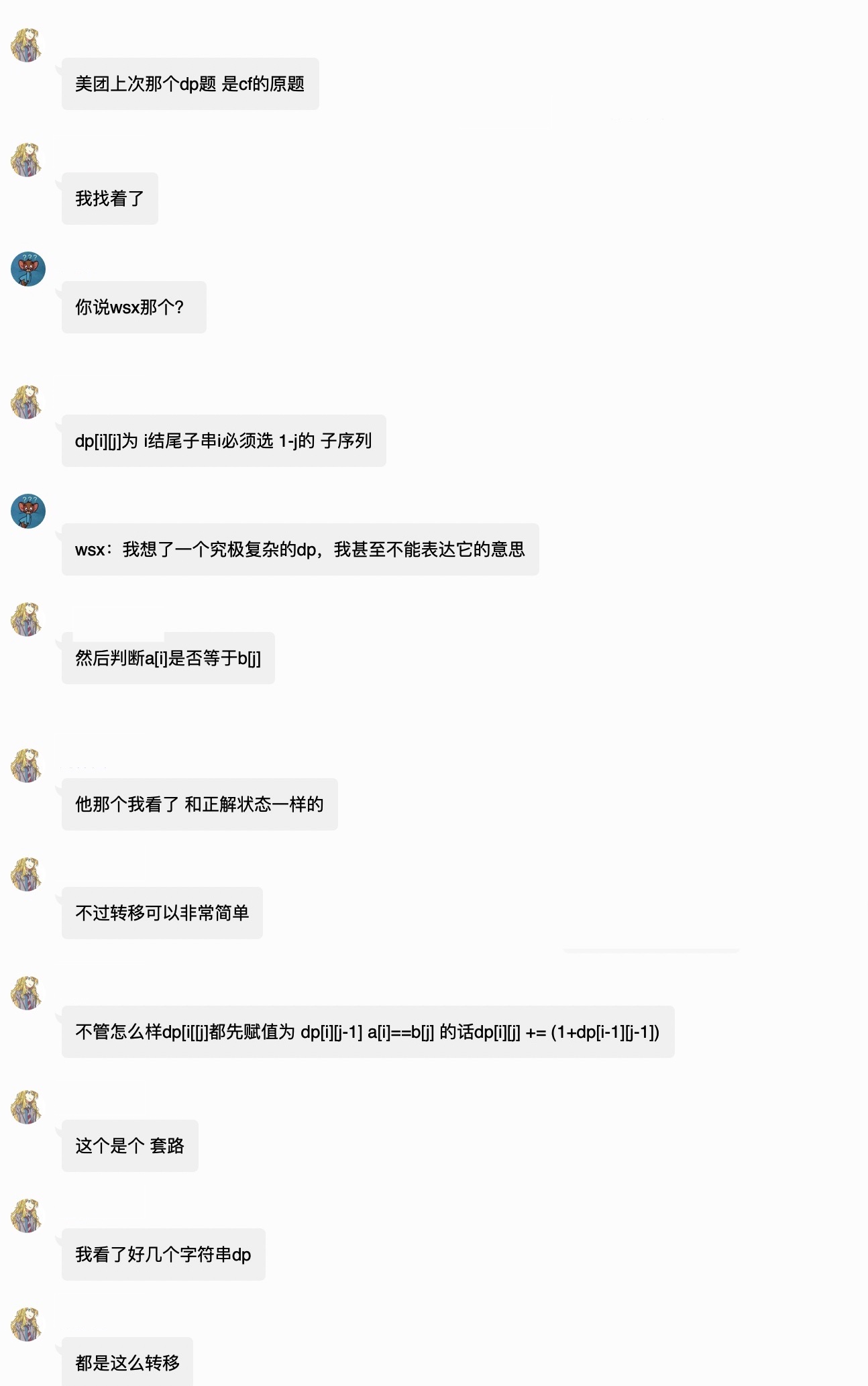

2020/4/17更新

一觉醒来挺多人找我要代码的，由于笔试的代码没有复制，所以我就重新敲一遍
##第二题

#include <iostream>
using namespace std;

const int N=1e5+5;
int pre[N];

int main(){
  long long a,b,x,m;
  cin>>a>>b>>x>>m;
  for(int i=0;i<3*m;i++){
    cout<<x<<" ";
    x = (a*x+b)%m;
    pre[x]=i;
  }
  cout<<endl;
  cout<<3*m-pre[(a*x+b)%m]<<endl;
}

第三题

#include <iostream>
#include <vector>
using namespace std;

typedef long long ll;

vector<ll> vec;
ll n,k;

ll maxrank(ll x,ll y){
  ll idx1 = lower_bound(vec.begin(),vec.end(),x)-vec.begin(); // vec[idx1] = x    idx1是最小的
  ll idx2 = upper_bound(vec.begin(),vec.end(),x)-vec.begin()-1; // vec[idx2] = x  idx2是最大的
  ll idy2 = upper_bound(vec.begin(),vec.end(),y)-vec.begin()-1;
  return (idx1-1-0+1)*n+(idx2-idx1+1)*(idy2-0+1);
  // 左边是第一个值小于自己的数的个数
  // 右边是第一个值等于自己的的数的个数
}

ll getidx(){
  ll l=0,r=n-1;
  while(l<r){
    ll mid = (l+r)/2;
    if(maxrank(vec[mid],vec[n-1])<k) l=mid+1;
    else r=mid;
  }
  return l;
}
ll getidy(ll idx){
  ll l=0,r=n-1;
  while(l<r){
    ll mid = (l+r)/2;
    if(maxrank(vec[idx],vec[mid])<k) l=mid+1;
    else r=mid;
  }
  return l;
}


int main(){
  cin>>n>>k;
  for(ll i=0;i<n;i++) {
    ll x;
    cin>>x;
    vec.push_back(x);
  }
  sort(vec.begin(),vec.end());
  for(ll i=0;i<n*n;i++){
    k = i+1;
    ll idx=getidx();
    ll idy=getidy(idx);
    cout<<vec[idx]<<" "<<vec[idy]<<endl;
  }
}

第五题

#include <iostream>
using namespace std;

const int N=5555;
const int mod = 1e9+7;
int dp[N][N];
int sum[N][N];
int size[N][26];
string s,t;
int n,m;

// aaa
// aaa
// a 3*3 = 9
// aa 3*2 = 6
// aaa 1
// ans = 16

int main(){
  cin>>s>>t;
  int n = s.size();
  int m = t.size();

  for(int i=0;i<n;i++){
    for(int j=0;j<m;j++){
      sum[i][j] = 0;
      if(i>0) sum[i][j] += sum[i-1][j];
      if(i>0&&j>0&&s[i]==t[j]) sum[i][j] += dp[i-1][j-1];
      sum[i][j] %= mod;
    }

    for(int j=0;j<26;j++) {
      if(i>0) size[i][j] = size[i-1][j];
    }
    size[i][s[i]-'a']++;

    for(int j=0;j<m;j++){
      dp[i][j] = size[i][t[j]-'a'] + sum[i][j];
      dp[i][j] %= mod;
    }
  }

  int ans = 0;
  for(int j=0;j<m;j++) ans = (ans+dp[n-1][j])%mod;
  cout<<ans<<endl;
}

本文作者： fightinggg
本文链接： http://fightinggg.github.io/yilia/yilia/Q8VYLN.html
版权声明： 本博客所有文章除特别声明外，均采用 MIT 许可协议。转载请注明出处！