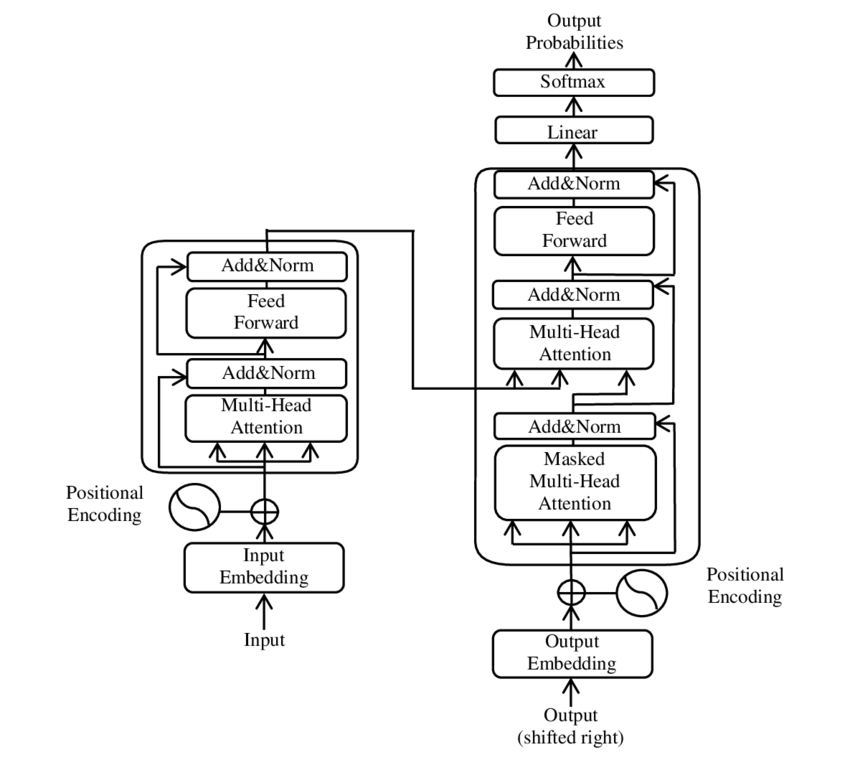
Transformer
Transformer背景介绍
Transformer指的是一种架构,未来的NLP(自然语言处理)都可以使用此架构。Transformer由编码器、解码器(后面会介绍)等组成,他的输入是向量数组,输出是也是向量数组。
注意:Transformer架构的输出是把向量逐个输出的。
Transformer架构最初只用来做机器翻译,例如将英语翻译成德语。在翻译的过程中待翻译语句作为输入,而翻译结果作为输出。待翻译语句中的每一个Token(词)会被转化为向量作为输入,Transformer的输出向量最终被转化为翻译结果的Token(词)。由于Transformer逐一输出结果的特性,翻译结果是一个Token(词)一个Token(词)逐渐输出的。
Transformer架构不仅仅只可以用与机器翻译,Transformer现在也用于GPT中,就是GPT的最后一个字母T所代表的含义。由于Transformer逐一输出结果的特性,GPT也是一个Token(词)一个Token(词)逐渐输出的。
注意力机制
注意力机制源自做翻译时的技巧,当我们翻译某个词的时候,我们应该注意这个词。例如我们如果要翻译以下句子为中文:
1 | Hello World ! |
假设他的标准答案是:你好,世界!
当我们写下中文你好的时候,我们需要注意单词Hello,因为这个单词将被翻译成你好,当我们写下中文世界的时候,我们需要注意单词World。注意力机制就试图让机器明白以上道理。
更加严谨一点,在训练时,用公式表示即为:假设已知输入为向量数组$K$包含向量$K_1$,$K_2$,$K_3$等。假设预期输出为向量$V$包含向量$V_1$,$V_2$,$V_3$等,已知注意力为$A$,$A_{ij}$代表$V_i$的计算中,$K_{j}$所占的权重。
那么便有了计算公式$V_i=F(f_{i1},f_{i2},f_{i3}…)$,$f_{ij}=f(A_{ij},K_{j})$, 注意其中的$F$函数和$f$函数,如何设定都可以。
在测试时,假设一个测试数据为向量$Q$包含$Q_1Q_2Q_3$, 按照$V$的计算公式,其中只有$A$需要变更,因为$A_{ij}$代表$V_i$(而不是$Q_i$)的计算中,$K_{j}$所占的权重。这里只需要想办法换成想要的注意力即可,方法有很多,主要围绕$Q$和$V$的相似关系来计算,这里不做展开。下文介绍一种使用自注意力机制的方案来计算相似关系。
自注意力机制
自注意力机制源于另一个技巧,当我们翻译某个词的时候,我们应该注意另一个词。例如:
1 | The program has a bug |
当我们翻译bug的时候,不能把它翻译成虫子。我们需要注意到前面的单词program,因此翻译成问题
因此我们将一份训练数据的输入,即当做$K$,又当做$V$,也当做$Q$。于是就可以训练出前文说的注意力$A$
// TODO
多头自注意力机制
由于自注意力机制可学习的参数较少,多头自注意力机制用来扩充自注意力机制的可学习参数。
多头自注意力机制,将输入投影到$N$个不同的空间,得到$N$个输入,分别做自注意力机制,得到$N$个输出,最终通过全连接层投影回来,得到一个输出。
在这个过程中,产生了投影的参数、全连接的参数,可学习参数就多起来了。
位置编码
自注意力模型,不受位置的影响。考虑一个输入是向量数组,若打乱输入顺序,不影响输出结果,这个是不合适的,可以考虑直接把位置也编码进输入中,方案是使用三角函数给输入向量的每一个维度都加上周期的三角函数值。
为什么是三角函数?这是收到计算机中数字编码的启发。若把计算机中的32位数字的每一个位拿来看,从0到最大值,32位的每一个位都是周期不同的01变换(最低位变换为010101…,次低位是001100110011…,再次为000011110000111100001111…),这其实也是一种三角函数。
Transformer
// TODO
 x
x