总览
这篇博客将用于整理各种堆的数据结构代码以及复杂度证明: 二叉堆、二项堆、斐波拉契堆、配对堆、左偏树、斜堆、bordal队列、B堆
注意
全部代码单对象测试通过,部分代码未实现拷贝构造函数达到深拷贝。
heap
堆是一种非常重要的数据结构,在计算机科学中,堆一般指堆是根节点比子孙后代都要大(小)的一种数据结构。
项目地址
链接
前置条件
基本数据结构:变长数组、栈、队列、字符串的实现(此时暂未实现,使用STL代替,后面有时间会自己实现)
内存池机制
{ post_link 势能分析}
基类设计
在这里我们暂且只设置三个接口,如果不够,我们再补充。
heap代码
binary heap
二叉堆,就是我们常见的堆,也是大多数人常用的堆,二叉堆是一个完全二叉树,满足根节点的值大于(小于)子孙的值。我们设计他的时候,采取下标从1开始的数组来直接模拟,使用i,2i,2i+1之间的关系来完成边的构建。
push
我们将数放入数组尾部,并不断上浮即可。细节稍微推一下就出来了。每个元素最多上浮堆的高度次,复杂度$O(lgn)$
pop
我们直接删掉第一个元素,并让最后一个元素顶替他,然后下沉即可。这里个细节也是稍微推一下就出来了。每个元素最多下沉堆的高度次,复杂度$O(lgn)$
top
就是第一个元素,复杂度$O(1)$
代码如下:
binary heap代码
binomial heap
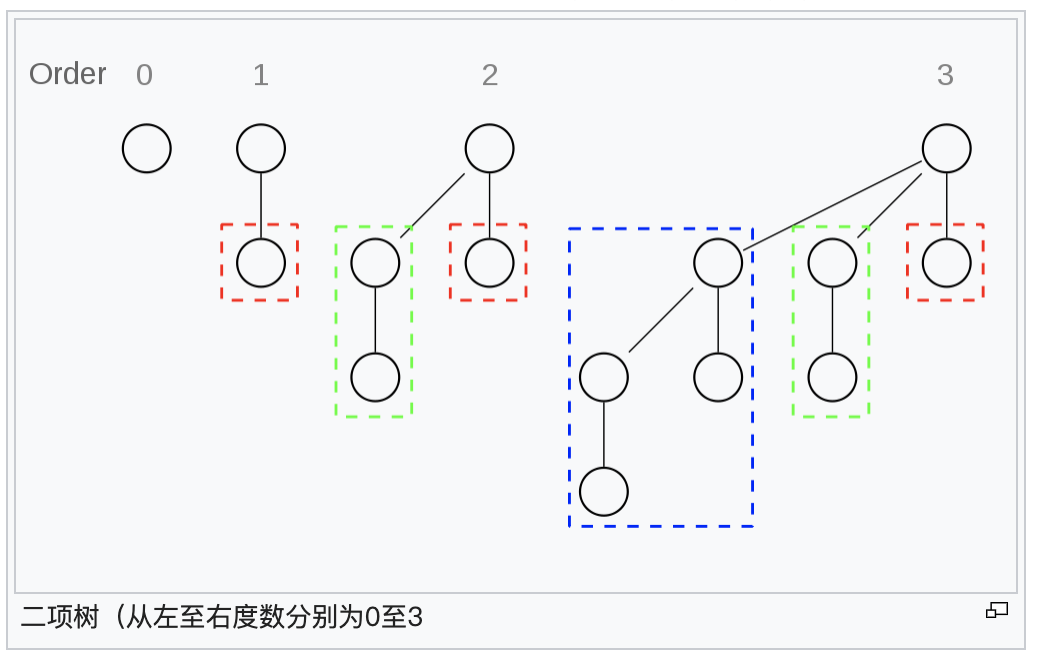
二项堆,是一个堆森林,其中每个堆以及各自的子堆的元素个数都是2的幂,并且森林中没有两个堆元素个数相同的堆。举个简单的例子,一个包含了6个元素的二项堆,这个堆森林中一定是两个堆组成,因为6=2+4,他不能是6=2+2+2由三个堆组成,因为森林中不允许出现元素相同的堆。
堆的具体形状
*** 图片源于wiki***
merge
二项堆天然支持合并,即可并堆,当合并的时候,我们很容易发现,只要将森林合并即可,而对于哪些出现的元素个数相同的堆,我们可以两两合并,让其中一个作为另一个的根的直接儿子即可。每次合并的时候,两两合并的复杂度是$O(1)$,最多合并的次数等于森林中元素的个数减1,而森林中堆的个数等于二进制中1的个数,这个是O(lgn)级别的,所以总体复杂度O(lgn)
push
可以看作与一个只包含了一个元素的堆合并,每次push,最坏的情况下时间复杂度为$O(lgn)$,但是多次连续的push,均摊时间复杂度就不一样了,我们来分析一下n次连续push的情况,森林中的堆两两合并的次数等于时间复杂度,定义函数$f(x)$,表示在森林中所有堆中的元素个数的总和为$x$的情况下,push一个值以后,堆中合并发生的次数,显然$f(x)=$x的二进制表示中末尾连续的1的个数,不难发现
$f(x)>=1$的时候$x%2=1$,
$f(x)>=2$的时候$x%4=3$,
$f(x)>=3$的时候$x%8=7$
这里我们通过计数原理推算出
$$
\begin{aligned}
\sum_{i=1}^n{f(i)}=\lfloor\frac{x+1}{2}\rfloor+\lfloor\frac{x+1}{4}\rfloor+\lfloor\frac{x+1}{8}\rfloor+…+\lt x+1
\end{aligned}
$$
所以在大量连续的push过程中,均摊时间复杂度为O(1)
pop
先遍历各个根,找出最值,不难发现,森林中,任意一个堆去掉根以后,恰好也是一个满足条件森林,这里也可以用合并处理,时间复杂度$O(lgn)$
top
遍历所有堆即可,时间复杂度O(lgn)
程序设计
很多人说用链表实现链接,这确实是一个好方法,但是如果用单链表或循环链表或双向链表实现,则有很多局限性,下面代码中也提及了。我这里采取的是使用数组存森林,使用左儿子右兄弟的手段,将多叉树用二叉树来表示。这个方法非常棒。
代码
binary heap代码
fibonacci heap
斐波拉契堆,是目前理论上最强大的堆,他和二项堆很长得很相似。和二项堆一样,斐波拉契堆也是一个堆森林,斐波拉契堆简化了几乎所有的堆操作为懒惰性操作,这极大的提升了很多操作的时间复杂度。
potential method
对于一个斐波拉契堆$H$,我们定义势能函数为$\Phi(H) = t(H) + 2m(H)$, 其中$t(H)$是斐波拉契堆$H$的森林中堆的个数,$m(H)$是斐波拉契堆中被标记的点的数量。
push
当我们向一个斐波拉契堆中添加元素的时候,我们会选择将这个元素做成一个堆,然后链入森林的根集和,常常选择链表维护根集合,同时更新斐波拉契堆中最小值的指针,实际时间复杂度显然是$O(1)$,势能变化为1,因为堆的个数变大了1,均摊复杂度为$O(1)+1=O(1)$
merge
当我们合并两个斐波拉契堆的时候,我们是懒惰操作,直接将这两个堆森林的根集合并为一个根集,常常选择链表来维护根集合,同时更新新的最小值指针,实际实际复杂度为$O(1)$,势能无变化,均摊复杂度为$O(1)$
top
$O(1)$
decrease
当我们想要减小一个节点的值堆时候,我们直接将他和父亲断开,然后将他链入森林并减小值,然后标记父亲,如果父亲被标记过一次,则将父亲和爷爷也断开并链入森林,并清除标记,一直递归下去,这里我们不要太认真,加上这条路上一个有$c$个,则我们一共断开了c次,实际复杂度为$O(c)$,势能的第一项变为了$t(H)+c$,第二项变为了$2(m(H)-c)$,于是势能的变化为$c-2c=-c$,于是均摊复杂度为$O(c)-c$,这里本来并不等于$O(1)$,但是我们可以增大势的单位到和这里的$O(c)$同级,这样就得到了$O(1)$
erase
当我们想要删除一个节点的时候,先将其设为无穷小,然后在调用pop
pop
前面偷了很多懒,导致除了erase以外,其他操作的均摊复杂度均为$O(1)$,这里就要好好地操作了,我们是这样来操作的,删掉最小值以后,将他的儿子都链入森林,这里花费了$O(D(H))$的实际代价,这里的$D(H)$指的是斐波拉契堆$H$中堆的最大度数。然后我们更新top的时候,不得不遍历所有的根,这时候我们就顺便调整一下堆。我们遍历所有的根,依次对森林中所有的堆进行合并,直到没有任意两个堆的度数相同,假设最后我们得到了数据结构$H’$,那么这个过程是$O(t(H)-t(H’))$的,于是时间复杂度为$O(t(H)-t(H’))+O(D(H))$,然后我们观察堆的势能变化,显然第一项的变化量为$t(H’)-t(H)$,第二项无变化,即势能总变化为$t(H’)-t(H)$,则均摊复杂度为$O(t(H)-t(H’))+O(D(H))+(t(H’)-t(H))$,这里依然不一定等于$O(D(H))$,但是我们依然可以增大势的单位到能够和$O(t(H)-t(H’))$抵消,最终,均摊复杂度成了$O(D(H))$
D(H)
现在我们进入最高潮的地方。我们考虑斐波拉契堆中一个度数为k的堆,若不考虑丢失儿子这种情况发生,我们对他的儿子按照儿子的度数进行排序,显然第i个儿子的度数为i-1,$i=1,2,3…k$,此时考虑儿子们会丢掉自己的儿子,则有第i个儿子的度数$\ge i-2$,在考虑他自己也会丢失儿子,但这不会影响到第i个儿子的度数$\ge i-2$这个结论。
斐波拉契数列
$$
\begin{aligned}
F_i =
\left{
\begin{aligned}
&0&i=0\
&1&i=1\
&F_{i-2}+F_{i-1]}&i\ge 2\
\end{aligned}
\right.
\end{aligned}
$$
斐波拉契数列的两个结论
$F_{n+2}=1+\sum_{i=1}^nF_i$
$F_{n+2}\ge \phi^n,\phi^2=\phi+1,\phi大约取1.618$
比斐波拉契数更大
容易用数学归纳法证明对于一个度数为k的堆,他里面的节点的个数$\ge F_{k+2}$,这里$F_{i}$是斐波拉契数列的第i项。
当k=0的时候,节点数数目为1,大于等于1
当k=1的时候,节点数数目至少为2,大于等于2
若$k\le k_0$的时候成立, 则当$k=k_0+1$的时候,节点数目至少为$1+F_1+F_2+…+F_{k_0+1}=F_{k_0+3}=F_{k+2}$
比黄金分割值的幂更大
现在我们就能够得到一个结果了,一个度数为k的堆,他的节点个数至少为$\Phi^k$,这里我们很容易就能得到这样一个结果,$D(H)\le \log_\Phi 最大的堆内元素的个数$
结尾
至此我们已经全部证明完成,读者也应该知道为什么斐波拉契堆要叫这个名字。
fibonacci heap 代码
fibonacci heap代码
pairing heap
配对堆,名字来源于其中的一个匹配操作。很有趣,他的定义就是一个普通多叉堆,但使用特殊的删除方式来避免复杂度退化。是继Michael L. Fredman和Robert E.Tarjan发明斐波拉契堆以后,由于该数据结构实现难度高以及不如理论上那么有效率,Fredma、Sedgewick、Sleator和Tarjan一起发明的。
potential method
我们有一个配对堆$H$,其中有n节点$node$,$node_i$有$d_i$个儿子,
则有
$F(H) = \sum F(node)$,
$F(node_i)=1-min(d_i,\sqrt{n})$
复杂度证明方面,等我把论文看完再来整这个,感觉证明比斐波拉契堆更复杂。
merge
合并的时候,让次大堆做最大堆的儿子,显然时间复杂度$O(1)$
push
插入的时候,看作与只包含了一个元素的堆合并,所以$O(1)$
top
就是根 $O(1)$
pop
当我们删除根以后,会形成一个堆森林,这时我们从左到右,每两个连续的堆配对合并一次,然后从右到左依次合并。比方说有这样一个情况AABBCCDDEEFFGGH,我们先将其从左到右合并AA->A,BB->B…得到ABCDEFG,->ABCDEH -> ABCDI -> ABCJ -> ABK -> AL -> M
程序设计
同样的左儿子右兄弟
代码
pairing heap代码
leftist heap
左偏树、左式堆、左翼堆是一个堆,除此以外,他定义了距离,没有右子节点的节点的距离为0,其他节点的距离为右子节点的距离加1,在这个定义下,左偏树的左偏体现着每个节点的左子节点的距离不小于右子节点的距离。
push
为新节点建立堆,然后与堆合并 $O(lgn)$
pop
删除根节点,合并左右子树 $O(lgn)$
top
根节点 $O(1)$
merge
$O(lgn)$, 当我们合并两个堆$H1,H2$的时候,我们只需要比较这两个堆顶的大小,不妨设H1小,并设H3、H4为H1的左右儿子,则我们可以这样来看待,我们将H3,H4从H1中断开,递归合并H4和H2位H5,这时候我们还剩下H3、H5以及H1的堆顶,我们根据左偏树的定义,选择H3、H5分别作为左右或右左儿子即可,
复杂度证明
算法中每次均选择右儿子递归向下,这导致时间复杂度与右儿子的右儿子的右儿子的…有关,这里不难发现递归的次数就是节点的距离。根据左距离不小于右距离,我们很容易就能得到这个距离是$O(lgn)$级别的。
leftist heap 代码
leftist heap代码
skew heap
我们的左偏树不记录距离,并且每次递归的时候无条件交换左右儿子,则成了斜堆。
复杂度证明
potential method
定义斜堆中的右子树距离比左子树大的节点为重节点,否则为轻节点。
定义势能函数为重节点的个数。
merge
当我们合并两个斜堆$H_1,H_2$的时候,不妨设他们的右子节点链中的轻重儿子为$l_1,h_1,l_2,h_2$,则时间时间复杂度为$O(l_1+h_1+l_2+h_2)$,经过交换以后,链上的重节点一定会变成轻节点,轻节点可能会变为重节点,我们取最坏的情况,即轻节点全部变为重节点,这时势能的变化量为$l_1+l_2-h_1-h_2$,最后我们的均摊复杂度为$O(l_1+h_1+l_2+h_2)+l_1+l_2-h_1-h_2$,我们依然可以增大势的单位,直到足以抵消所有的h,最终均摊复杂度为$O(l_1+l_2)$,这里不难证明,一条右儿子构成的链上,轻节点的个数是对数级别。
skew heap代码
skew heap代码
bordal heap
这里已经涉及到一些冷门的东西了。暂时先放一下
B heap
是一种和B树一样利用内存页的东西。冷门,先放一下
wiki上还有数不清的堆,学到这里暂停一下
)